When retiring, should you choose monthly pension payments or a lump-sum payment and invest it?
Unfortunately, many people (including financial advisors) take a somewhat lazy approach to this conundrum by failing to conduct a comprehensive analysis of the available options. This can lead to faulty decision making around a significant financial asset.
Fortunately, there is a robust and straightforward process for evaluating the pension vs. lump-sum decision. We start by “doing the math”.
Quantitative Analysis
Step #1 – Get Probability Weighted Future Cash Flows
It can be difficult to compare a stream of monthly pension payments with a lump-sum paid today. Many people may simply perform a standard breakeven analysis. For example, if your monthly pension payment is $1,000/month or $12,000/year, and your lump-sum payment is $100,000, then your breakeven period is 8.33 years ($100,000 ÷ $12,000/year). If you live longer than 8.33 years, you “win”, if not, you “lose.”
However, a breakeven analysis relies on a faulty assumption. Namely, that all monthly payments are equally likely to be received. In reality, the older we get, the less likely it is that we will receive a future pension payment.
If you are 65 years old today, then the chances of you being alive next month are much greater than the chances of being alive in 10, 20, or even 30 years. As a result, we must reduce the value of future payments by the probability of actually receiving them.
We can calculate the expected (or probability-weighted) value of future pension payments through the use of mortality tables.1 Simply put, mortality tables give us the odds that we will be alive or dead at some point in the future. From these tables, we can estimate the probability of being alive to receive a future payment and then calculate the appropriate probability-weighted cash flow value.
Let’s consider Jack as an example. Jack is a 65 year old male. Based on one popular mortality table, Jack has an 84% chance of being alive in 10 years (Jack’s age 75). So if Jack’s annual pension payment is $20,000, then we would multiply $20,000 x 0.84 = $16,800. This is the amount of money Jack can expect to receive in 10 years based on his life expectancy.
We would repeat this process for every year and create a table of expected cash flows. For Jack, it would look something like this:
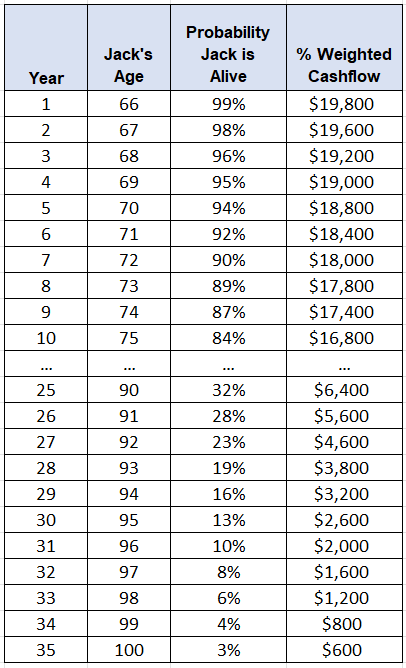
Step #2 – Discount Cash Flows
After obtaining the probability-weighted future cash flows, we must then “discount” them to the present using an appropriate interest rate.
As a simple example, here is what Jack’s discounted cash flows would look like assuming a 5% interest rate:

Choosing the correct interest rate can be difficult, but here are some general considerations:
- Employee of the US Federal Government? It’s appropriate to use the yield on US Treasuries.
- Employee of state/local government? It’s appropriate to use the yield on municipal bonds offered by the government entity, but with an adjustment made for disparate tax treatment (e.g. muni bond interest is tax free while pension payments are not).
- Employee of private employer? It’s appropriate to use the yield on the employer’s corporate bonds.
- What’s the funding status of the pension fund? An underfunded pension fund may require a higher interest rate compared to a fully funded pension fund.
Step #3 – Add It All Up
Now that we have all of the discounted cash flows, we simply add them all together. Then we can compare the total of the discounted cash flows with any lump-sum payout. In Jack’s example, the present value of taking lifelong payments is about $230,000. If Jack’s lump-sum option is $300,000, then it might make sense to take a lump-sum now. But if Jack’s lump-sum option is $200,000, then the stream of annual payments might be more attractive.
Consider Using a Calculator
In many cases (such as joint survivor options), “doing the math” can get very complicated. One helpful tool is an annuity factor calculator (AFC).2 An AFC can incorporate a wide range of variables and also allows you to quickly perform sensitivity analysis by adjusting any given input for the AFC.
One thing to note… an AFC calculates just that… an annuity factor. Put simply, an annuity factor is the relationship between the annual pension payment and the lump-sum. Using Jack’s example, he expects a $20,000 annual payment, which equates to a lump-sum of $230,000. Divide $230,000 by $20,000 and you end up with an annuity factor of 11.5.
When using the AFC, you would obtain the annuity factor, and multiply it by the expected annual pension payment to get the corresponding lump-sum equivalent amount.
Now that we’ve completed the quantitative analysis, we must look at the qualitative factors around the pension claiming decision.
Qualitative Considerations
When it comes to qualitative factors, I would start with the following questions:
How do you feel about the various payment options?
Are you worried about any latent health conditions?
Are you committed to investing a lump-sum in a disciplined manner for a long period of time? Or will you be tempted use the lump-sum amount to buy a new boat, car, etc.?
What is your backup plan if the pension fund were to default on their obligations and stop/reduce payments?
How will the pension integrate with your other sources of retirement income?
Are your other investments conservative or risky?
How will the various payment choices affect your current and future tax picture?
Armed with the cold, hard numbers from Step #1, you can use these questions to start a conversation around the benefits and drawbacks of the various pension payment options as they relate to your personal situation and preferences.
Going back to Jack one last time, let’s imagine his pension fund offers a lump-sum option of $250,000 (vs. the $230,000 expected value for the pension payments). Obviously, $250,000 is more than $230,000. But what if Jack is worried he might squander his lump-sum? In this case he would “give up” $20,000 of expected value by forgoing the lump-sum and accepting the annual pension payments. Does that make sense? For Jack, it might!
But what if the lump-sum is $300,000? Now we have a $70,000 difference, and it becomes a bit harder for Jack to decide (obviously it’s unlikely that such a large difference will exist, but it’s a helpful illustration around the thought process). In this case, maybe he can accept the lump-sum, use part of the lump-sum to buy a fixed annuity that might approximate his pension payments and then spend any remainder on that new boat or car.
The important thing to remember is that there is no right/wrong answer, only one that makes sense for your personal situation and preferences.
And as with most financial planning decisions, we must be comfortable with uncertainty. All of the analysis in the world can’t guarantee that we realize the optimal outcome (the crystal ball is foggy). But by using the framework described above, it’s possible to make a high-quality and well reasoned decision.
1There are a variety of helpful mortality tables available either through the Social Security Administration or the Society of Actuaries.
2You can find a great annuity factor calculator here: https://afc.soa.org/

